We acknowledge that there are the physics of software which we cannot change
- Software is not magic
- Software is never “done”
- Software is a team effort; nobody can do it all
- Design isn’t how something looks; it is how it works
- Security is everyone’s responsibility
- Feature size doesn’t predict developer time
- Greatness comes from thousands of small improvements
- Technical debt is bad but unavoidable
- Software doesn’t run itself
- Complex systems need DevOps to run well
From Tom Limoncelli; his post goes into great detail
Git
Today I was honoured to be able to share about Git as part of the Front End Development South Africa’s work with Keep The Receipt.
If you would like to see it, it will be on YouTube soon (will link to it here) and the slides are immediately available.
OWASP TOP 10
Recently been talking a lot about the OWASP Top 10 and have created some slides and a 90 min talk on it!
So if want to raise up your security, this is a great place to start.
Smarter Screen
I spend a lot of time in the kitchen, I love to cook and so I am often in there with my phone listening to a podcast or, if it is a Saturday morning, watching Show of the week. I am not alone in this behaviour, everyone in my home does this and often at dinner we share youtube videos by propping a phone up on the toaster and huddling around it. This was clearly time to improve the experience with a kitchen screen - a smart TV would be perfect but their lack of support means it is a show stopper for me… so I put together a smarter screen.
Build List
Powering this is a Raspberry Pi 4. I grabbed the 4Gb model, just cause… I don’t have a smart reason for that decision. If you are in South Africa, I grabbed mine from PiShop and grabbed the essentials kit. Putting together the “case” was maybe the most head-scratching aspect since it is just screws, plastic and a fan… no instructions.
Also ordered from PiShop was the remote control since I want this to be like a TV, I do not want a keyboard or mouse. I opted for the OSMC Remote Control which has a small USB dongle and uses radio signals rather than infrared, which means it does not need line of sight. Since the Pi will be behind the screen, the line of sight will be an issue. The remote “just worked” which was so awesome.
For the screen, I ordered a LG 24MK400H which was the perfect side for my needs, wall-mountable and on special 😄 The mounting solution I grabbed a Brateck LDA18-220 Aluminum Articulating Wall Mount Caravan Bracket, which is really awesome and easy for mounting. This came with instructions but they were poor and going with experimenting first helped me find a happier setup.
With all of that, I had everything I needed to get running.
OS
The Pi kit came with a MicroSD card with NOOBS preinstalled on it and all I needed to do is when booting, hold shift and select the LibreElec OS to install. LibreElec is a really basic OS which is “just enough” to run the Kodi media centre software. Going through the setup on that got it up and running within about 30min.
Add-ons
I don’t have a “library” of media, rather I just stream the content I want so installing the add-ons I needed was key to set up, and I went with:
- YouTube
- TubeCast, this lets me cast from my phone to the Kodi
- Twitch
- Amazon Prime Video (VOD), this is for streaming Amazon and not for the buying of movies
- Netflix, this has a really great guide to getting started with 3rd party add-ons which are worth your time
Notes
The only strange part of the setup was that each time the Kodi booted, I got a prompt saying there is an update for LibreElec… but the settings for LibreElec had nothing in it for the update and no way to do the update. Thanks to Reddit I was able to switch it to manual and update the setup and then switch it back.
Go to Settings > LibreELEC > System. Change automatic updates to ‘manual’ (I’m not even sure if auto update works at all, I’ve had it set to that before and it never auto updates). Change update channel to LibreELEC-8.0. Select available versions and select the newest one (8.2.3 at time of writing this).
If this was how you were trying to update, then I’m not sure. I would say backup your LibreELEC install and then start fresh with a new version.
DevFest 2019
Today I was honoured to be part of the second DevFest in SA with a talk sharing about Kotlin, Micronaut, DataStore and other fun tech... but more on how we ended up where we are with our current project. It is a tech lead doing a retrospective with tech sprinkles to get everyone involved.
If you want the code it is on GitHub and slides are below:
When the world sees a 500... but the server promises it is a 200
Here is the story of all the work I did this week, and it is so odd I feel it needs to be shared… but lets talk about the world the problem can be found in.
The world
It is a µservice (that is the ohh, look how smart I am to use a symbol for micro) written with DropWizard and deployed in a Docker container, with Traefik in front of that. To hit it you go through a ingress controller and a load balancer.
+---------------+
| |
| Internet |
| |
+---------------+
|
|
|
+---------------+
| |
| Load Balancer |
| |
+---------------+
|
|
|
+---------------+
| |
| Ingress |
| |
+---------------+
|
|
|
+---------------+
| |
| Traefik |
| |
+---------------+
|
|
|
+---------------+
| |
| Microservice |
| |
+---------------+
The microservice acts a BFF (backend for front end), so it does some auth fun and makes calls to an internal API and manipulates them (e.g. changes the data structure). We have a number of different REST style calls across GET, POST, PUT and DELETE.
In terms of environments, we obviously have a production environment and we have an integration environment which are setup the same way. We have a stubs environment where we fake out the internal API. Lastly we can run the microservice on our laptops, but there is just the microservice… no traefik etc…
The Problem
When we run our load test from outside everything works except 1 call which fails 98% of the time with a HTTP 500. Other calls (even the same method) all work. Load tests run against the stubs environment and the same call works perfectly on our laptops, in integration and production.
We can even run the fake internal API on the laptops, with the load tests and it works fine there. Basically, one call fails most of the time in one environment… 🤔
Grabbing logs
When we pull the logs for the microservice in stubs things get weirder… it is returning an HTTP 200 😐 This is the same experience we get everywhere else, it works… except in stubs to the load tests it gets a 500
+---------------+ 500 Here
| |
| Internet |
| |
+-------+-------+
|
|
/
|
|
+-------+-------+ 200 Here
| |
| Microservice |
| |
+---------------+
Further pulling of logs show 500s in the load balancer and the ingress so somewhere between the microservice and traefik the HTTP 200 becomes a HTTP 500… but we don’t have logs on traefik we can pull which makes this a bit harder to determine…
Logging onto Traefik
Next we logged onto Traefik and decided to curl the microservice directly and lo and behold… we get a 500 🤯 and to make it more interesting that the microservice logs still show it is returning a 200 - like what the actual?! Could there be an network issue or magic?
Interesting the 500 came with an error saying “insufficient content written”
Insufficient content written
This led me to looking at the content and looking at what we are sending and I see we are sending Content-Length and the body and guess what… the length of the body does not equal the Content-Length… oh 💩
This is a client side HTTP error… where the server sends the incorrect amount of body, so the client goes, well the server is wrong and raises a 500. I’ve always thought 500 errors were server error and thus could only be raised on the server.
The fix
The fix is simple, in our server we were using the Response.fromResponse to map internal API to the public API and so it was copying the Content-Length from the internal API and we were sending that along.
This meant the fix was to delete the Content-Length header before we call fromResponse to ensure it would rebuild the header and be correct.
The reason why it didn’t fail else where, the version of the mock API we use added Content-Length but newer versions and the real APIs used chunked encoding which never set the header so there is no issue there.
This was a long road to understand the issue, and one line to fix it, and totally a new experience in learning that server errors can occur client side too.
VSCode + Catalina
 For the most part, the initial upgrade to macOS Catalina was uneventful; I was caught unaware by the wave of permission requests that greeted me but it was 2 minutes of clicking accept or deny and continuing on with my day (though, how normal users will cope is beyond me... it feels very un-apple).
For the most part, the initial upgrade to macOS Catalina was uneventful; I was caught unaware by the wave of permission requests that greeted me but it was 2 minutes of clicking accept or deny and continuing on with my day (though, how normal users will cope is beyond me... it feels very un-apple).
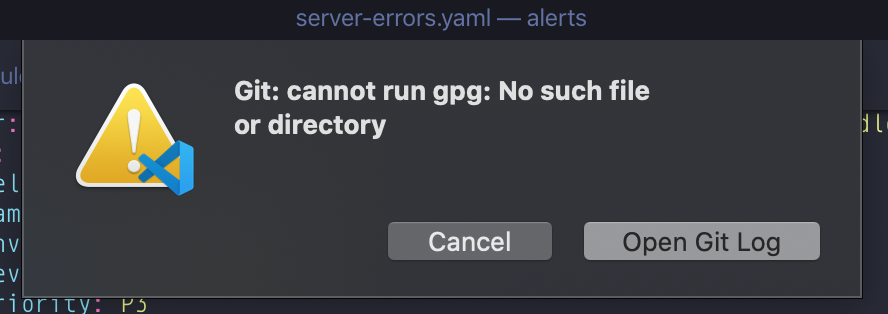
The two issues I did run into, were the need to reconfigure Google Drive (again, a minor 2-minute activity) and trying to get VSCode to work properly. This was a lot more annoying. The initial issue was that git, could not be found… this broke all of source control in VSCode. The fix was to run the following from the terminal: xcode-select --install and restarting VSCode.
Once that was fixed, the next issue was that I could no longer sign commits with GPG, this gave a similar issue as the initial Git not being found.
The correct fix for VSCode is to add it to the list of Developer Tools which you can find under Security & Privacy. Once a restart of VSCode everything just worked. I added Terminal to the list too which also stopped autocomplete from Fish Shell from constantly prompting too.
important reminder that diversity is important
(I tweeted this story today, and some wanted to be able to share it so here it is)
Everyone gets along well at work, except Jim
He never comes to after-work drinks. He doesn’t go get Friday burger lunch with the team. He doesn’t chip in for Sarah’s farewell gift. When he gets unicorned (i.e. he left his machine unlocked & someone emailed everyone), he doesn’t buy the punishment cake. This annoys everyone. Why doesn’t he just play along? It is harmless fun.
Jim sucks… Right? He just isn’t trying to be part of the team… Right?
Well, Jim can’t afford the transport from after-hours drinks or the expensive burgers or the cake.
He would like to.
Financial diversity is a hard one to spot in a team, but it is a real thing. Are you excluding people because they are not privileged like you?
Learning Kotlin: The notnull delegate and lateinit
- This is the 30th post in a multipart series.
If you want to read more, see our series index - This follows the introduction to the
byoperator and delegates
A lot of introductions to Kotlin start with how null is opt-in because that makes it safer, we even looked at this way back in post 8. The problem though is that sometimes we do not know what we want the value to be when we initialise the value and we know that when we use it we don’t want to worry about nulls. The ability to change from null to never null might seem to be impossible but Kotlin has two ways to do the impossible.
Before we look at the two solutions, let us look at a non-working example. Here we have a class to represent a physical building and we want to store the number of floors which we get from calling an API (not shown). The problem here is there is no good default value. A house with just a ground floor is 0, a multistory office building could have 10 floors, and an underground bunker could have -30 floors.
class Building() {
var numberOfFloors : Int
fun getBuildingInfo(erfNumber : String){
// call municpality web service to get details
numberOfFloors = 0; // 0 cause 0 = G like in elevators
}
}
fun main(args:Array) {
val house = Building()
house.getBuildingInfo(“123”)
println(“My house, up the road, has ${house.numberOfFloors}”)
}
This will not compile as it states Property must be initialized or be abstract for the number of floors.
notnull
Following on from our previous delegates we have the notnull delegate we can use to allow the property to not be set initially and then
import kotlin.properties.Delegates
class Building() {
var numberOfFloors : Int by Delegates.notNull()
fun getBuildingInfo(erfNumber : String){
// call municpality web service to get details
this.numberOfFloors = 10;
}
}
fun main(args:Array) {
val house = Building()
house.getBuildingInfo(“123”)
println(“My house, down the street, has ${house.numberOfFloors}”)
}
This example will print out that we have 10 floors. If we were to comment out line 14, we would get the following exception: Exception in thread "main" java.lang.IllegalStateException: Property numberOfFloors should be initialized before get. - so not exactly a null exception but close enough it makes no difference.
lateinit
Another option is lateinit which we can add before the var keyword, but we cannot use it with Int, or other primative types so we need to change that as well to a class. This is a really nice and simple solution.
data class Floors(val aboveGround: Int, val belowGround: Int)
class Building() {
lateinit var numberOfFloors : Floors
fun getBuildingInfo(erfNumber : String){
// call municpality web service to get details
this.numberOfFloors = Floors(2, 40);
}
}
fun main(args:Array) {
val house = Building()
house.getBuildingInfo(“123”)
println(“My house, in the middle of the avenue, has ${house.numberOfFloors}”)
}
Once again, if we comment out line 14 we get an exception as expected ‘Exception in thread “main” kotlin.UninitializedPropertyAccessException: lateinit property numberOfFloors has not been initialized’.
lateinit vs. notnull
As we can see in our simple examples both achieve the goal but they both have their own limitations and advantages too:
-
notnullbeing a delegate needs an extra object instance for each property, so there is a small additional memory/performance load. - The
notnulldelegate hides the getting and setting in a separate instance which means anything that works with the field, for example Java DI tools, will not work with it. -
lateinitdoesn’t work with primitive types (Int, Char, Boolean etc…) as we saw above. -
lateinitonly works withvarand notval. - when using
lateinityou gain access to the.isInitializedmethod which you can use to check if it was initialized.
Learning Kotlin: The vetoable delegate
- This is the 29th post in a multipart series.
If you want to read more, see our series index - This follows the introduction to the
byoperator and delegates
The vetoable delegate is usable with variables only (i.e. you need to be able to change the value) and it takes a lambda which returns a boolean. If the return value is true, the value is set; otherwise, the value is not set.
As an example, we will have a User and ensure the age can never be lowered (since time only goes forward)
import kotlin.properties.Delegates
class User() {
var age : Int by Delegates.vetoable(0) { property, oldValue, newValue ->
newValue > oldValue
}
}
fun main(args:Array<String>) {
val user = User()
user.age = 10;
println(user.age)
user.age = 15
println(user.age)
user.age = 10
println(user.age)
}
This produces:
10 15 15
